Algebraically decaying interactions
One of the fundamental question that pertains to spin models governed by long-ranged interactions is the influence of the interaction range on their critical behavior. Two of the most challenging issues when investigating these models by means of stochastic (Monte Carlo) methods are:
- the onset of a diversity of phase transitions as the decay parameter is varied, and
- a large algorithmic complexity stemming from the huge number of interactions between spins and the presence of an extra parameter in the phase diagram of the models.
We have considered in particular algebraically decaying interactions, i.e., with no intrinsic length scale. This class of potential has drawn increasing interest in the last decades:
- in condensed matter physics, for the microscopic modeling of a variety of real systems including, but not limited to, magnetic thin films or magnetic nanoparticles incorporating dipolar interactions (with or without an F/AF competition), highly ionic systems (weak or no screening), Josephson junction (in connection with the Kondo effect) and systems governed by RKKY interactions;
- in transport phenomena, in connection with Lévy flights and abnormal diffusion processes, owing to the existence of powerful maps between kinetic models with Lévy flight dynamics and equilibrium spin models;
- on the border between physics and information theory/processing, e.g., neural networks and complex graphs, image processing or coding, due to the fact that one can reexpress a large collection of these problems as (equilibrium) disordered spin models.
- from the perspective of critical phenomena and the renormalization group, where long-ranged potentials serve as a powerful laboratory framework for the investigation of the influence of the interaction range on the nature of phase transitions; this includes tests of epsilon-expansions (through the alteration of the effective dimension of the model) or the investigation of cross-overs between universality classes.
Generalized ensembles Monte Carlo methods
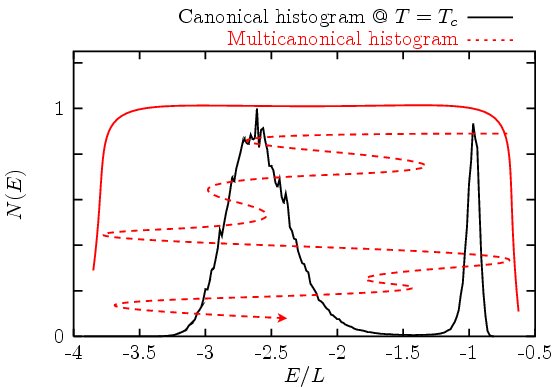
We explore the critical behavior of these systems by means of stochastic methods operating in generalized ensembles, i.e., methods that directly compute the density of states (or a variant thereof) instead of sampling the microstates of the system using a Boltzman weight (as is the case with the famous Metropolis algorithm). Basically, generalized ensemble methods work by sampling the configurations of the system in an (abstract) auxiliary ensemble, e.g., the multicanonical ensemble (leading to flat histograms of some macroscopic variables), the 1/k-ensemble (yielding higher occurences of low-energy configurations) or the optimized ensemble (ensuring enhanced diffusion at critical energies). In the case of multicanonical methods, the resulting dynamics engendered by the Markov chain is that of a random walker diffusing along the axis of a given macroscopic variable, generally the energy (although other variables may be used for that purpose, e.g., the Parisi overlap parameter in the case of spin glasses). This kind of dynamics ensures that free energy barriers are efficiently overcome, which is a serious leap forward wrt to previous methods when one wants to study systems with complicated energy landscapes (e.g., glassy and/or frustrated systems, polymers, …) or exhibiting first-order transitions (Fig. below: 8-state Potts model below, at, and above the transition).

This is achieved by replacing the usual Boltzman weight exp(-E/kT) by a so-called multicanonical weight exp(-S(E)), where S(E) is the microcanonical entropy (the logarithm of the density of states), so that the resulting energy distribution n(E) exp(-S(E)) is flat. Since the entropy is initially unknown, such algorithms work by estimating the density of states in an iterative way and at the same time using this estimate to enlarge the region of the phase space being sampled, until a flat energy distribution is eventually reached. Once the density of states has been estimated, thermodynamic averages can be straightforwardly obtained by performing a so-called reweighting operation.
Historically, generalized ensemble methods appeared in the mid 90’s in the context of polymers, protein folding or spin models (with special emphasis on the 2D Potts model and the EA spin glass model), but have since then been generalized to quantum phase transitions (for instance, the stochastic series expansion for bosonic systems) or lattice quantum field theories (in combination with multigrid methods). Every time you come across highly repetitive dynamics, you may want to think about switching to one of the currently available generalized ensembles schemes.
Link to my Java applets illustrating how the iterative Wang/Landau algorithm works.
Finite-size effects and phase diagram of the long-range Potts model
We have investigated the phase diagram of a long-range, q-state Potts chain. In the short-range case, this model exhibits either a first- or a second- order transition, depending on the lattice dimension and the number of states $q$. With long-ranged interactions of the form 1/r^alpha, there are subtle critical effects that do not otherwise occur, including a Kosterlitz-Thouless transition for alpha=2. In addition, the fact that every particle “feels” the boundaries gives rise to unusual finite-size effects [1,4]. This model has been the subject of intense controversy since the mid-90’s, in particular where the nature and location of phase transitions is concerned (first- vs second- order, KT-like, crossover to the exact mean-field or the short-range behavior).
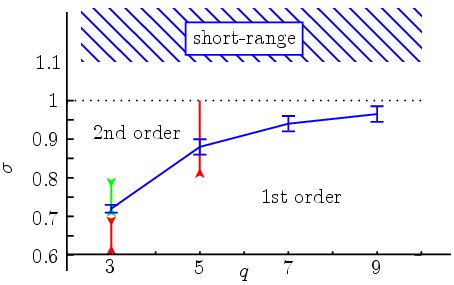
We have shown that this model exhibits a phase diagram made of a tricritical line alpha(q) separating the first- and second- order regimes, and computed the location of this line with an unprecedented two-digits accuracy [2] by means of new discriminating method based on the location of spinodal points [1]. On the line of inverse square interactions, we also observed a very unusual finite-size effect: while the transition seems to be first order at finite lattice size, it becomes a continuous transition in the thermodynamic limit. This result settled a long-standing controversy surrounding the nature of the phase transition on this line, and suggests that finite-size scaling at first-order transitions is in general highly atypical in long-range models. Beyond this line, the behavior of the model was shown to turn into a short-range one within a narrow window, lending clear support to a long-suggested renormalization group scenario [1]. In a recent article [4] we have shown the existence of an unusual crossover in the finite-size scaling behavior of response functions when the transition is of the first order. Here again, the fact that in long-range models, surface effects do not vanish (with respect to bulk behaviors) as rapidly as in short-range models when the lattice size is increased leads to unusual physics that may also be of interest in systems of nanometric size.
Cluster updates in the multicanonical ensemble and investigation of the fractal geometry of the interface
Most of my recent results were obtained by means of collective-update version of the multicanonial algorithm [3,4]. We devised this method with the aim of scrutinizing finite-size scaling effects, which in the case of long-range potentials imposes simulating systems over at least two decades of lattice sizes. Our method builds on the ability of cluster algorithms to rapidly reduce temporal correlations, and relies upon the microcanonical temperature to bridge the gap between multicanonical ensembles and random-cluster representations. Owing to its straightforward formulation, it can be used in a variety of multicanonical implementations, including the Wang-Landau algorithm [3] and the Transition Matrix method [4]. Systematic tests demonstrate the superiority of this method over standard multicanonical methods: the numerical accuracy is drastically improved, and the reduction of the algorithm complexity to that of a short-range model of the same linear size ensures remarkable scalability.
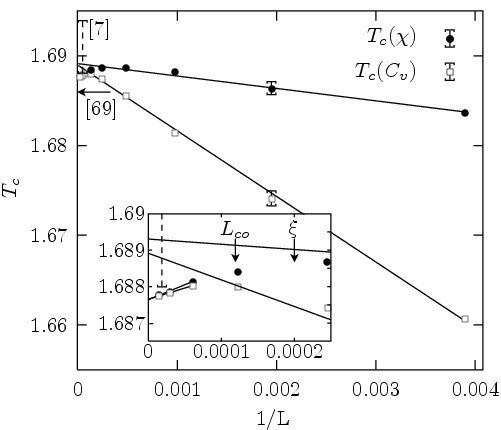
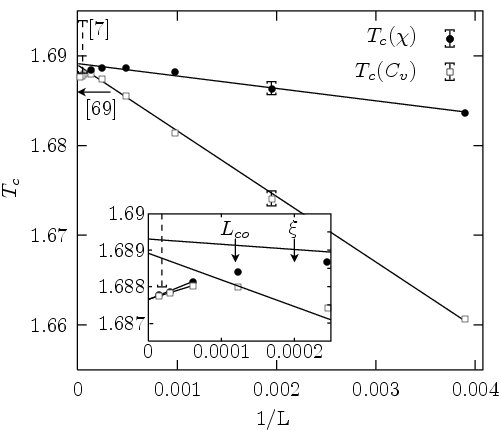 Finite Size Effects in the LR Potts model: The investigation of finite-size effects permitted by this methods (Fig. above) has shown important finite-size corrections, and suggests that the mixed-phase interface has a fractal dimension depending on the decay parameter of the interaction [4]. We provided an estimate of the correlation length that is consistent with this picture.
Finite Size Effects in the LR Potts model: The investigation of finite-size effects permitted by this methods (Fig. above) has shown important finite-size corrections, and suggests that the mixed-phase interface has a fractal dimension depending on the decay parameter of the interaction [4]. We provided an estimate of the correlation length that is consistent with this picture.Finally, the benefits of the method extend far beyond the realm of long-range models: the estimate of the surface tension for the two-dimensional nearest-neighbor Potts model (up to 256 x 256 spins) matches the exact value to an accuracy never attained with Monte Carlo methods, although modest statistics were used.
Long-range potentials in the presence of disorder
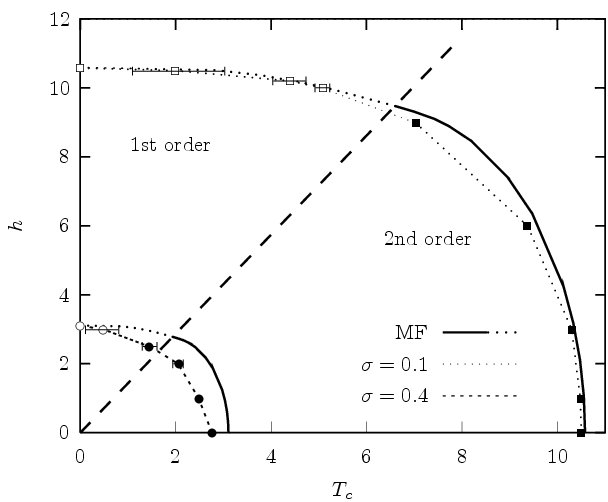
Here we focus on the extension of this method to disordered models, in particular the long-range Ising chain with bimodal random fields. This model constitutes a perfect framework for the test of RG derivations, owing to the ability to alter the effective dimension in a continous way. In [5,6], we have shown that a discontinuous transition sets on at large fields for slowly decaying interactions. This is consistent with a similar scenario reported in the nearest-neighbor version of this model. In order to improve the sampling of the phase space, I am currently developping a multi-walker version of the Wang-Landau multicanonical algorithm combined with the two-replica cluster method of Machta/Newman/Chayes.
Spin-dependent transport in AF-coupled bilayers
With Khalid Akabli (2005-2009, adv. H. T. Diep) we developed a Monte Carlo simulator for the investigation of spin-dependent transport in a multilayer with antiferromagnetic interlayer exchange coupling [7].
Related Publications
- S. Reynal and H.T. Diep, Phys. Rev. E 69, 026109 (2004): Reexamination of the long-range Potts model: a multicanonical approach (preprint)
- S. Reynal and H.T. Diep, J. Appl. Phys. 95, 6968 (2004): Q-state Potts model with power-law decaying interactions: along the tricritical line (preprint)
- S. Reynal and H.T. Diep, Comp. Phys. Comm. 169 (243), 2005: Hybrid Multicanonical Cluster Algorithm for Efficient Simulations of Long-Range Spin Models (preprint)
- S. Reynal and H.T. Diep, Phys. Rev. E 72, 56710, 2005: Fast Flat Histogram Algorithm for Generalized Spin Models (preprint)
- S. Reynal and H.T. Diep, Random-field Ising chain with power-law decaying interactions (in preparation)
- These de doctorat: tel.ccsd.cnrs.fr (chapter I contains a review of the considerable literature that the study of long-range models has produced during the last three decades)
- K. Akabli, H.T. Diep and S. Reynal, Spin transport in magnetic multilayers, J. Phys.: Condens. Matter 19, 356204 (2007) (preprint).
